Diseños de logos a partir de figuras giradas
Figura imposible obtenida por el giro de un polígono regular.
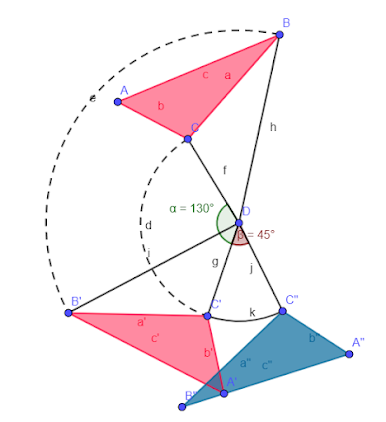
Si transformamos el triángulo superior de color rojo en el inferior de color rojo mediante un giro de 130º y tomamos el mismo centro O para transformar mediante otro giro en el mismo sentido el triángulo azul vemos que podemos obtener mediante un giro de la suma de las amplitudes de esos ángulos, el triángulo azul a partir del primero.
Podemos deducir en consecuencia que el producto de dos giros de mismo centro es como resultado otro giro de igual centro y cuyo ángulo es la suma de los ángulos utilizados para ambos giros.

El producto de dos simetrías de ejes concurrentes es un giro

A la izquierda, el producto de dos simetrías de ejes concurrentes es un giro mientras que a la derecha observamos que, el producto de dos simetrías de ejes paralelos es una traslación.
Giro de triángulosMover los puntos ABCD para ver los casos distintos y particulares de un giro de 200º a la derecha (sentido horario) de un triángulo.
De centro, ángulo y sentido dado es un movimiento que desplaza el elemento con una distancia constante alrededor del centro.
Giro: es una rotación aplicada bajo cierto ángulo desde un centro que transforma cada punto en otro de manera que la distancia del centro a ese punto es invariable. Si el ángulo de giro vale 180° tenemos una simetría central. El centro es el único elemento invariante salvo el giro identidad, por ejemplo el giro de una figura 360° o 0º.
Producto_de_giros. - GeoGebra Hoja Dinámica
Producto de giros de mismo centro.
Mover los puntos ABCD para ver los distintos casos.
Si giramos una figura desde un centro y luego otro ángulo añadido bajo el mismo centro, el resultado es un giro en el que se suman los dos ángulos. En el dibujo el triángulo se gira primero 120º (del rosa al azul) y luego 90º (del azul al verde) obteniendo el tercer triángulo que respecto al primero ha girado 210º, la suma de ambos.
Por tanto:
Producto de giros: el producto de dos giros de ángulos o amplitudes distintas bajo un mismo centro es un giro de amplitud de ambos ángulos sumados bajo el mismo centro.
 Giro a la izquierda del triángulo desde el c
entro O. Como todos los puntos giran el mismo ángulo, los sectores circulares que definen su arco son todos proporcionales.
 Giro a la izquierda del triángulo azul que se transforma tras el movimiento en el triángulo verde.
 Cuando una figura gira en un plano tenemos que sus puntos siguen una trayectoria en forma de circunferencia, girando todos el mismo ángulo en torno a un punto. Cuando una figura gira en el espacio todos los puntos también giran el mismo ángulo pero cada punto gira sobre una circunferencia que es perpendicular al eje de giro y cuyo centro de giro está en el centro de esa circunferencia. Para calcular un giro de la figura C, que se apoya al igual que la cuña -de la que tomamos una arista como eje de giro- en el mismo plano, construimos el giro espacial de cada punto, de esta manera tomamos desde un punto A de la figura una recta m perpendicular al eje de giro y por el plano perpendicular al eje de giro que pasa por ambos puntos AP, trazamos la otra recta m’ que corresponde junto a la anterior m al ángulo girado m-m’, transformando A en A' mediante el giro. Hacemos lo mismo con los demás puntos y obtenemos la misma figura en su nueva posición tras el giro.
http://sistema-diedrico.blogspot.com/2010/11/giros.html

Dados dos prismas, uno de color verde y otro en color amarillo, el de color amarillo es un prisma en forma de cuña que utilizamos una de sus rectas oblicuas (la hipotenusa del triángulo rectángulo de una de sus caras) como eje de giro. Ambos prismas están apoyados en un plano y el prisma de color verde se gira respecto al eje de giro siguiendo una trayectoria circular tal y como aparece en el dibujo. Si consideramos un punto del prisma verde, por ejemplo el número 10, gira respecto al eje según un círculo perpendicular al eje de giro, de esta manera aparecen en el dibujo cada 36° la figura como quedaría hasta cubrir la circunferencia completa (los 360°). En el dibujo se puede observar la posición del prisma al ser girado en ángulos iguales respecto al eje de rotación. Cada punto del prisma gira según una circunferencia cuyo plano es perpendicular al eje de giro.
Giro en el espacio Si la figura tridimensional se levanta del suelo tenemos un giro en el espacio, claramente la figura ya no se mueve en torno a un punto sino que lo hace en torno a una recta, cada punto describe un arco de circunferencia cuyo plano es perpendicular al eje de revolución. El giro de una figura espacial siempre es un giro en el espacio, y en este caso se ve más claro porque la figura apoyada en un plano se separa de él tras el giro respecto al eje de giro para volver al mismo plano.
Giro en el plano o giro en el espacio Como podemos observar en la animación, un prisma que tiene una cara apoyada en un plano gira en torno a un centro que es el punto de tangencia donde se apoya la esfera. La figura, pese a ser un sólido tridimensional, gira en el plano y todos los puntos de la figura que están por encima de la base giran según un plano paralelo al anterior. Se entiende que los puntos de la cara superior están girando en un plano paralelo al del suelo y que por tanto cada punto obtiene su nuevo punto girado respecto a un centro de giro que está por encima del anterior, de lo cual hay que concluir que en realidad el giro de toda la figura se hace respecto a un eje vertical, no a un punto como se viene haciendo en un giro en el plano. En consecuencia, pese a que la base de la figura se mueve siguiendo un giro en el plano definido por el giro plano de la base, al ser una figura espacial que se mueve en torno a un eje en este caso vertical, tenemos que denominarlo giro en el espacio. |
|
Giros distintos centros otro giro - GeoGebra Hoja Dinámica
Giros de distintos centros generan otro giro: si giramos una primera figura obteniendo una segunda y ésta la giramos de nuevo desde otro centro obtenemos una tercera figura que puede obtenerse de la primera mediante un giro. Para calcular el centro de giro que transforma la primera en la tercera, hacemos los segmentos AA'' y CC'' y hacemos sus mediatrices, en la intersección de éstas está el centro de giro.
|

















No hay comentarios:
Publicar un comentario