sábado, 16 de octubre de 2010
Movimientos o transformaciones isométricas: traslaciones, giros y simetrías.
Giros
Diseños de logos a partir de figuras giradas
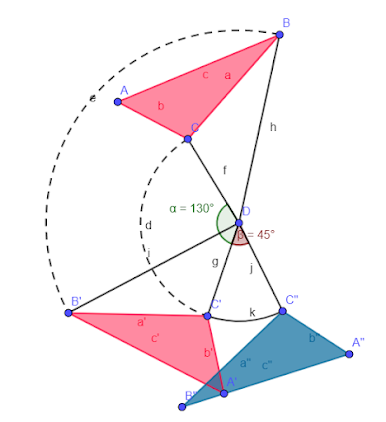
Si transformamos el triángulo superior de color rojo en el inferior de color rojo mediante un giro de 130º y tomamos el mismo centro O para transformar mediante otro giro en el mismo sentido el triángulo azul vemos que podemos obtener mediante un giro de la suma de las amplitudes de esos ángulos, el triángulo azul a partir del primero.
Podemos deducir en consecuencia que el producto de dos giros de mismo centro es como resultado otro giro de igual centro y cuyo ángulo es la suma de los ángulos utilizados para ambos giros.
Si hacemos un giro que transforma la figura ocre de la izquierda en la figura naranja central mediante un ángulo de 90º y hacemos otro giro de manera que convertimos la figura central en la figura violeta de la derecha mediante otro giro de 30º observamos que podemos transformar el primero en el tercero mediante un giro cuyo centro es en realidad la intersección de las dos mediatrices que definen los puntos de los lados de las figuras transformadas y el ángulo es la suma de ambos, esto es, 120º.
Giro de triángulosMover los puntos ABCD para ver los casos distintos y particulares de un giro de 200º a la derecha (sentido horario) de un triángulo. De centro, ángulo y sentido dado es un movimiento que desplaza el elemento con una distancia constante alrededor del centro. Giro: es una rotación aplicada bajo cierto ángulo desde un centro que transforma cada punto en otro de manera que la distancia del centro a ese punto es invariable. Si el ángulo de giro vale 180° tenemos una simetría central. El centro es el único elemento invariante salvo el giro identidad, por ejemplo el giro de una figura 360° o 0º.
|
Giros de distintos centros generan otro giro: si giramos una primera figura obteniendo una segunda y ésta la giramos de nuevo desde otro centro obtenemos una tercera figura que puede obtenerse de la primera mediante un giro. Para calcular el centro de giro que transforma la primera en la tercera, hacemos los segmentos AA'' y CC'' y hacemos sus mediatrices, en la intersección de éstas está el centro de giro. |
Traslaciones
Si transformamos el trapezoide violeta mediante una traslación en el trapezoide verde y a continuación realizamos un giro de centro aleatorio F para obtener el trapezoide naranja, observamos que podemos transformar el trapezoide violeta en el naranja mediante un giro cuyo centro queda en la intersección de las mediatrices de las rectas que definen cada par de puntos de los lados las figuras transformadas. Como consecuencia tenemos que el producto de una traslación y un giro es otro giro. Si transformamos un triángulo en otro mediante una traslación y este último en otro, mediante otra traslación podemos observar que podremos transformar el primero en el tercero mediante otra traslación, en consecuencia se puede establecer que el producto de dos traslaciones es otra traslación. TraslaciónMovimiento que desplaza cada punto según una dirección y sentido dados. Traslaciones: si un vector se transforma en otro de manera que conserva la misma longitud, dirección y sentido, tenemos una traslación en la que ningún punto permanece invariante salvo que sea una traslación de identidad.
|

Dadas tres rectas, (en el dibujo en color rojo), dos de ellas paralelas y un triángulo ABC, (en el dibujo en color rosa), se trata de realizar las transformaciones pertinentes para que la figura se convierta en un triángulo cuyos vértices incidan sobre las tres rectas. Trasladamos la figura dada en una dirección cualquiera hasta transformar el segmento CB en el segmento GH, para ello hacemos una recta por el vértice B con una dirección cualquiera hasta que corta a la recta EM en el punto G, por éste hacemos una recta paralela a la recta CB hasta que corte a la recta paralela a GB que pasa por C. Tenemos de esta forma el segmento trasladado GH con su base sobre la recta roja y lo giramos tomando como centro G hasta que corte a la recta DF en el punto I. Hemos por tanto trasladado el triángulo rosa y hemos girado su lado CB hasta obtener su nuevo lado IG a partir del cual construimos el triángulo equilátero IGJ. A partir de ahora sólo hay que trasladar este triángulo de color verde en la dirección de las rectas paralelas dadas, para ello hacemos una recta paralela por J a la recta FD hasta que corte a la recta DE, obteniendo de esta forma el punto K. Por este punto K hacemos dos los paralelas KL KM a los lados JG JI del triángulo verde obteniendo los otros dos puntos M L del triángulo azul buscado.
giro y traslación |
Simetrías
Simetrías A la izquierda, si hacemos la simétrica del triángulo ocre obtenemos el triángulo verde, si volvemos a hacer la simétrica del triángulo verde respecto a un eje obtenemos el triángulo violeta. Como podemos observar en el dibujo al aplicar dos simetrías axiales podemos transformar la primera a la tercera figura mediante un giro, por lo que podemos establecer que el producto de dos simetrías de ejes concurrentes es en realidad un giro como resultado final. A la derecha observamos como los ejes dejan de ser concurrentes y por tanto son paralelos, en consecuencia tenemos que el triángulo azul se transforma por simetría en el triángulo ocre y por otra simetría axial éste último se transforma en el rojo, el resultado final o producto obtenido es un triángulo rojo en el último caso en el que se transforma a partir del primero mediante una traslación, por tanto el producto de dos simetrías de ejes paralelos podemos decir que es una traslación. Podemos observar que mediante una simetría axial transformamos el cuadrado verde en el violeta y mediante otra simetría axial transformamos el violeta en el rojo, por tanto verificamos que el producto de dos simetrías axiales de ejes concurrentes provocan un giro cuyo centro es la intersección de los dos ejes de simetría, ya que podemos transformar el cuadrado verde en el rojo mediante un giro, tal y como observamos en el dibujo. El producto de dos simetrías de ejes concurrentes es un giro cuyo centro es la intersección de los ejes.
Una secuencia de números: 1
1 2 3 5 8
13 21 llamada de Fibonacci, es la que se obtiene
cada número sumando los dos anteriores, esta relación entre los números aparece
por doquier en la naturaleza, en los pétalos de una flor, en las conchas de los
moluscos y caracoles, en espirales de crecimiento exponencial, en el
crecimiento de las hojas a través de el tallo de una planta, etc. Es una serie
que se tiene en la suma de los dos últimos números, empezamos por el uno, lo
repetimos, y tenemos que su suma es dos, sumamos estos dos últimos, 2 + 1 igual
a tres, volvemos a sumar los dos últimos, 3 + 2 igual a cinco, y así
sucesivamente.
Esta relación entre cada par de números que escojamos de la
serie aparece continuamente en la naturaleza, en los tallos de ciertas plantas,
en los pétalos de las flores, en una estrella de mar, en una galaxia espiral,
detrás de la sucesión se esconde otro número, un número áureo y es aquel que sintetiza
la belleza de lo que nos rodea, un número cuyo valor es 1,618033, es el llamado
número de oro, además es el resultado de dividir dos números cualesquiera de la
serie anterior, cuanto más altos sean los números de la serie que escojamos,
más nos aproximamos a ese número de oro.
Muchas medidas de la naturaleza guardan esa relación, por
ejemplo nuestra altura dividido entre la distancia del suelo hasta el ombligo
da como cociente el número de oro, el ángulo áureo sale al representar estos
dos segmentos en una circunferencia: describe
el orden de las hojas de una palmera, de las pipas de un girasol, de las
escamas de una piña, del cociente entre los lados de la espiral del agua que se
vierte por el desagüe del lavabo, etc.
Nuestro mundo es pura geometría a todas las escalas, es el
lenguaje matemático del universo, de la belleza.
La simetría es el lenguaje de la naturaleza, el abejorro del
jardín puede distinguir las formas simétricas de las flores y es atraído por
ellas y es más probable que tengan alimento las flores más simétricas, y estas
son las que propagan mejor el polen, estas flores que son más simétricas atraen
mejor a las abejas. Las personas también
son atraídas por rostros más simétricos, un rostro simétrico es un detalle que
nos da información acerca de un buen ADN y de un buen proceso de desarrollo, lo
que comunica que somos una buena pareja si tenemos unas facciones simétricas.
Hay simetría en las rocas, en los objetos naturales, en el
universo, la simetría es eficaz, una pompa de jabón es esférica, es eficaz,
tiene un bajo consumo energético, la esfera es el cuerpo más simétrico, sirve
para compactar objetos y darles fuerza, un cráneo tiende a ser esférico para
ser más resistente a los golpes. Los diamantes son resistentes por que el
carbono está dispuesto en forma de tetraedro, y esa simetría es enormemente
resistente ya que el tetraedro regular tiene un amplio número de simetrías. Los
virus son simétricos para una mejor replicación, el virus puede realizar muchas
copias de sí mismo y la simetría se lo facilita.
Los diagramas son estructuras con organizaciones casi
siempre simétricas, son elementos que condensan ideas científicas, por ejemplo
el diagrama de Copérnico sobre el sistema heliocéntrico, el sol en el centro
del universo fue una idea revolucionaria, Copérnico simplemente trasladó la
idea con un diagrama muy simple, demostrando que los hombres no son el centro
del universo, el diagrama del principio del libro lleno de fórmulas lo resume
todo lo que es el sistema del universo descubierto por Nicolás Copérnico.
Un diagrama plasma una idea, ello sirve para descubrir los
patrones de un mundo aparentemente caótico, el orden dentro del caos, las
imágenes que nos muestran los diagramas trascienden las culturas, son un
lenguaje universal que se puede entender en cualquier lado del universo.
Un número primo es un número indivisible, todos los números
se forman multiplicando los primos entre sí, 3 × 5 × 7 es igual a 105. Esto es
un patrón, aunque no conocemos una fórmula que nos facilite obtener cualquier
número primo.
Un número primo es aquel que al dividirlo por otro da un
número fraccionario, excepto si lo divides por un número igual o por el uno.
Los primos son a los números como los átomos a la materia,
al igual que cualquier cosa se puede dividir en átomos, cualquier número se
puede dividir en números primos.
No existe una fórmula matemática para saber cuál será el
siguiente número primo en una serie. No existe una regla como la serie de
Fibonacci, aunque sabemos que existen infinitos números primos, Euclides lo
demostró.
Las matemáticas consisten en la búsqueda de patrones,
seguramente hay algún patrón en los números primos, pero a fecha de hoy es un
misterio. Hay patrones energéticos en los átomos grandes como los del uranio,
que comparten propiedades con los patrones de los números primos, es un patrón
marcado que no puede ser una coincidencia, las matemáticas de la física
cuántica puede que nos hagan descubrir el secreto de los números primos. Ello
podría tener consecuencias devastadoras para Internet, para la criptografía de
Internet, ya que algunas propiedades de los números primos encriptan claves de
las tarjetas.
La palabra simetría proviene del griego y significa
mensurado, adecuado, proporcionado, de proporción apropiada, de medida
conveniente también en el momento oportuno, e indica la posición que ocupan las
partes de un todo entre sí. La simetría está dada por la relación bella de una
parte como de las partes con el todo. Su expresión manifiesta se encuentra en
la repetición regular de motivos y circunstancias similares o iguales, parecidas
o afines. La simetría provee la base natural para un ordenamiento sistemático
de la variedad de todas las formas. Para evidenciar la simetría se utilizan
operaciones de superposición, por medio de estas operaciones o movimientos, las
cosas cuya simetría se desea analizar se superponen consigo mismas mediante
cambios de posición. Para el estudio de la simetría se utiliza en forma análoga
al álgebra, los recursos de las matemáticas como la teoría de grupos, de
acuerdo con sus métodos la simetría estructura y clasifica la variedad de
posibles formas efectivas teniendo en cuenta su clase y cantidad, la teoría de
grupos de transformaciones busca invariantes o elementos invariables dentro de
las transformaciones, son patrones que definen la estructura del grupo.
Los verdaderos órganos de simetría son aquellas figuras
geométricas que producen operaciones de superposición, por ejemplo en el octavo
no regular, la recta perpendicular a un plano que pasa por el centro de la
figura es un órgano de simetría, eje de rotación de orden ocho denotado con el
símbolo D8.
Existen numerosas operaciones de superposición y composición
que estructuran las simetrías, por ejemplo, la identidad es la representación
invariable de un objeto sobre sí mismo, con objetos que se transforman en sí
mismo, la traslación es un corrimiento simple bajo una dirección dada en línea
recta, la rotación es el giro de un cuerpo alrededor de un punto si es en el
plano y un eje si es en el espacio, la reflexión puede ser central o axial
dependiendo de si el objeto mantiene sus distancias en cada uno de sus puntos
respecto a un centro o respecto a un eje. Existe una reflexión especular en el
espacio respecto un plano. Una simetría radial es aquella que se engendra al
girar un elemento en torno a un centro. Una rotación por traslación es aquella
que engendra un punto de una hélice, una recta acoplada a ese punto genera un helizoide.
Podemos componer todos estos elementos y principios geométricos obteniendo
nuevas simetrías, por ejemplo una reflexión +1 traslación, un giro +1
traslación, una simetría +1 giro, etc.
Simetría centralMover los puntos ABCD para ver los casos distintos y particulares.
Simetría central: 2 puntos A-A’ son simétricos respecto a un 3º punto O cuando al trazar una recta que pasa por los 3 se tiene OA= OA’. Un ejemplo práctico de simetrías es el que se produce en los espejos.
|
Dos simetrías centrales con distinto centro es una traslación: dos simetrías centrales que transforman una figura primera en otra segunda y ésta en otra tercera, la primera se puede transformar en la tercera mediante una traslación.
|

|
Dado un punto B y dos rectas verdes (una de ellas sobre él), determinar un punto H sobre la recta BA que equidiste de B y de la recta AD.